Wed, 20 Aug 2008
Just Drawing Stuff on the Screen.
Richard Jones laments that drawing stuff on the screen is harder than it should be. I haven't seen his code, but it looks like he might be trying to do it with Ocaml and GTK which probably is more difficult than it should be. GTK isn't really meant for that sort of stuff.
Fortunately, there is a really well designed and thoroughly thought out library for doing graphics called Cairo, which even has a really great set of Ocaml bindings. On Debian/Ubuntu, the Cairo bindings can be installed using:
sudo apt-get install libcairo-ocaml-dev
I messed about with Ocaml and Cairo about a year ago and came up with this little demo.
(*
** http://www.e-dsp.com/what-are-fourier-coefficients-and-how-to-calculate-them/
**
** http://en.wikipedia.org/wiki/Fourier_series#Definition
*)
type fourier_series_t =
{ a0 : float ;
an : float array ;
bn : float array ;
}
let initial_size = 200
let two_pi = 8.0 *. atan 1.0
let sum_float_array ary =
Array.fold_left (fun x y -> x +. y) 0.0 ary
let calc_series max_n ary =
(*
** This uses a rough numerical approximation to integration.
** As long as the array is long enough (say 1000 or more elements), the
** results should be reasonable.
*)
let len = float_of_int (Array.length ary) in
let calc_Xn trig_func n =
let n = n + 1 in
let ary = Array.mapi (
fun i x -> x *.
trig_func ((float_of_int (n * i)) *. two_pi /. (len -. 1.0))
) ary
in
2.0 *. (sum_float_array ary) /. len
in
let a0 = (sum_float_array ary) /. len in
let an = Array.init max_n (calc_Xn cos) in
let bn = Array.init max_n (calc_Xn sin) in
{ a0 = a0 ; an = an ; bn = bn }
let waveform_of_series outlen series =
(*
** Given a fourier series, calculate a single cycle waveform of the
** specified length.
*)
let calc_point i =
let x = two_pi *. (float_of_int i) /. (float_of_int (outlen - 1)) in
let asum = sum_float_array (Array.mapi (
fun i an -> an *. (cos (float_of_int (i + 1) *. x))) series.an
)
in
let bsum = sum_float_array (Array.mapi (
fun i bn -> bn *. (sin (float_of_int (i + 1) *. x))) series.bn
)
in
series.a0 +. asum +. bsum
in
Array.init outlen calc_point
let fold_over_clipped_sine gain len =
let point i =
let x = gain *. sin (two_pi *. (float_of_int i) /. (float_of_int len)) in
if x > 1.0 then x -. 2.0
else if x < -1.0 then x +. 2.0
else x
in
Array.init len point
let redraw w series _ =
let cr = Cairo_lablgtk.create w#misc#window in
let { Gtk.width = width ; Gtk.height = height } = w#misc#allocation in
Cairo.save cr ;
( Cairo.identity_matrix cr ;
let border = 20.0 in
Cairo.move_to cr border border ;
Cairo.line_to cr border (float_of_int height -. border) ;
Cairo.stroke cr ;
let wave_width = width - 100 - (int_of_float border) in
let middle = float_of_int height /. 2.0 in
let wave_height = 0.7 *. (middle -. border) in
Cairo.move_to cr border middle ;
Cairo.line_to cr (border +. float_of_int wave_width) middle ;
Cairo.stroke cr ;
Cairo.move_to cr (border +. float_of_int wave_width) border ;
Cairo.line_to cr (border +. float_of_int wave_width)
(float_of_int height -. border) ;
Cairo.stroke cr ;
Cairo.set_source_rgb cr 1.0 0.0 0.0 ;
let wave_data = waveform_of_series wave_width series in
Cairo.move_to cr border (float_of_int height /. 2.0) ;
Array.iteri (fun i x ->
Cairo.line_to cr (border +. float i)
(middle -. wave_height *. x))
wave_data ;
Cairo.stroke cr ;
) ;
Cairo.restore cr ;
true
let () =
if Array.length Sys.argv != 2 then
( Printf.printf "Usage : %s <series length>\n\n" Sys.argv.(0) ;
exit 0 ;
) ;
let series_len = int_of_string (Sys.argv.(1)) in
let w = GWindow.window ~title:"Fourier Series Demo" ~width:600 ~height:400 () in
ignore (w#connect#destroy GMain.quit) ;
let b = GPack.vbox ~spacing:6 ~border_width:12 ~packing:w#add () in
let f = GBin.frame ~shadow_type:`IN ~packing:(b#pack ~expand:true ~fill:true) () in
let area = GMisc.drawing_area ~width:initial_size ~height:initial_size
~packing:f#add ()
in
let array_len = 1000 in
let wave = fold_over_clipped_sine 1.2 array_len in
let series = calc_series series_len wave in
ignore (area#event#connect#expose (redraw area series)) ;
w#show () ;
GMain.main ()
The above code can be compiled using:
ocamlopt -I +cairo -I +lablgtk2 cairo.cmxa lablgtk.cmxa cairo_lablgtk.cmxa \
gtkInit.cmx fsdemo.ml -o fsdemo
and the output looks like this:
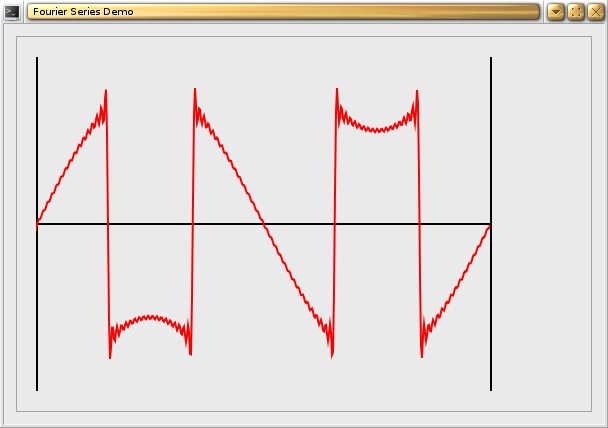
So while I agree that the 140 of lines of code here is about 30 times as much as Richard's code from his ZX80 days, I also think the results are at least 30 times as good.
Posted at: 22:29 | Category: CodeHacking/Ocaml | Permalink

![[operator<< is not my friend]](http://yosefk.com/c++fqa/images/operator.png)
